Taking an example from Markov Analysis, we have:
| This Month | Next Month | |
| Vevi | Kevi | |
| Vevi | 0.7 | 0.3 |
| Kevi | 0.1 | 0.9 |
A brand switching problem where the customer buys clothes every month from either of the two brands (Vevi or Kevi). The probabilities are transition probabilities representing the shift of customer from one brand to another in month-1.
The matrix thus obtained is called transition matrix. As we discussed, the elements of the row are mutually exclusive & collectively exhaustive (MECE).
We have at our disposal the probabilities of transition of month-1. What if we needed to calculate the probability of customer buying from Kevi in month-2, given he bought from Vevi in month-0?
Using the most basic concepts of probability theory, we construct a decision tree:
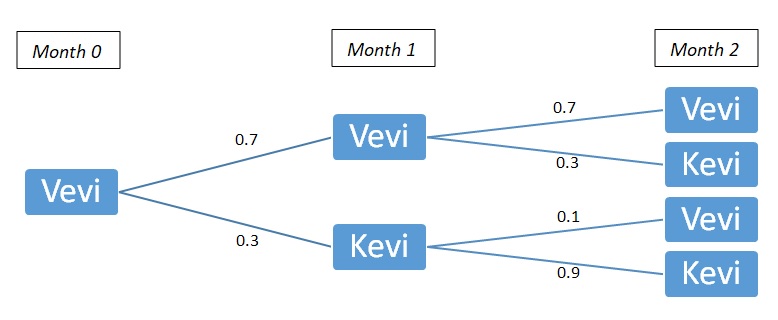
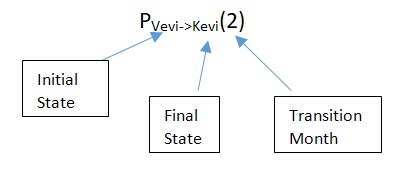
Denoting our subject probability as follows:
Therefore, PVevi->Kevi(2) = 0.7 X 0.3 + 0.3 X 0.9 = 0.21 + 0.27 = 0.48
Also, PVevi->Vevi(2) = 0.7 X 0.7 + 0.3 X 0.1 = 0.49 + 0.03 = 0.52
Similarly,
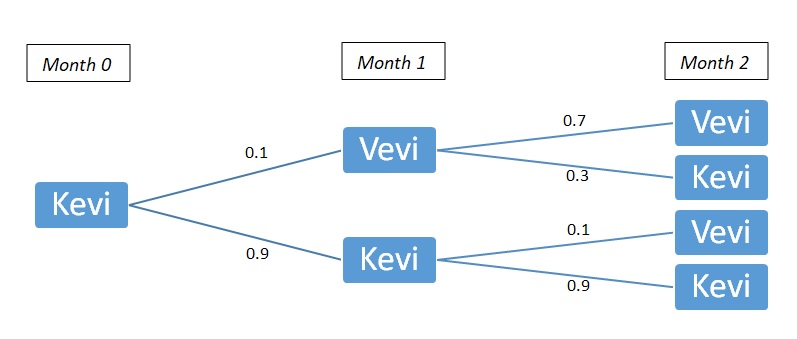
PKevi->Vevi(2) = 0.1 X 0.7 + 0.9 X 0.1 = 0.07 + 0.09 = 0.16
PKevi->Kevi(2) = 0.1 X 0.3 + 0.9 X 0.9 = 0.03 + 0.81 = 0.84
| This Month | Month 2 | |
| Vevi | Kevi | |
| Vevi | 0.52 | 0.48 |
| Kevi | 0.16 | 0.84 |
This Transition Matrix is MECE as well.
What if raised the initial Transition Matrix to power 2?
Let us call initial matrix as T(1).
Which is similar to previous matrix. Thus, we have an extremely important property of transition matrix.
T(n) = T(1)n
That is, the n-step transition probabilities are the elements of the nth power of the n-step transition matrix.
