Prisoner's Dilemma

Prisoner's Dilemma is another game theory model which shows how rivals could act to their mutual disadvantage. This explained by the pay of matrix of two prisoners X and Y who are both party to a certain crime for which they are being interrogated separately. Since X and Y cannot communicate, there is uncertainty in the mind of each one about the behaviour of the other. During interrogation each prisoner is told that:

• If both X and Y confess, both will be given a jail term for 5 years.
• If no one confesses, then for lack of evidence, each may be convicted for a minor crime and both X and Y get a 2 years jail term.
• If Y confesses but X does not confess, then Y will get a term of only 1 year while X will go to jail for 10 years, and
• If X confesses but Y does not confess, then X gets jail for 1 year while Y will get 10 years imprisonment.

These outcomes are illustrated in the pay off the two prisoners. Proposition (i) where both X and Y confess and each gets 5 years term is proposition (ii) where none confesses and get 2 years term each proposition (iii) where Y confesses but X does not confess and so X gets 10 years and Y only 1 year term. Box C proposition (iv) when X confesses but Y does not confess, so X gets 1 year but Y gets 10 years jail term.

In this uncertain situation, if chooses to confess, he faces two possibilities,
(i) Y may also confess and this X face 5 year jail term and
(ii), Y may not confess and thus X gets 1 year term.

But if X does not confess, but Y confesses, then X is bound to get a 10 years sentence. The other prisoner Y too is faced with a similar dilemma. If both X and Y do not confess then each one will get lowest sentence of two years and thus both of them will gain. But X is uncertain of how Y would behave and thus to avoid maximum sentence, X decides to confess thus resulting in 10 years jail for Y. so to avoid maximum sentence. Thus uncertainty about behaviour of the other causes both of them to have got a lighter sentence. Uncertainty about each other's behaviour has thus resulted in mutual disadvantage.

We can apply the conclusions of 'prisoners dilemma' to the behaviour of oligopoly firms X and Y. suppose, these two firms arrive at some price agreement and honestly enforce it they will be acting as a collusive monopoly, and will be earning monopoly profits or high profits. But if any one cheats and charges a low price it will earn very high profit. This lure to earn very high profits often leads to such cheating by the members of a cartel. The situation the two oligopoly firms are:

• If cheats but X does not cheat, then Y gets very high profits and X gets very low profits.
• If X cheats and Y does not cheat, then X gets very high profits and Y gets very high profits and Y gets very low profits.
• If none of them cheats, then both get high profits (as distinct from very high profits).
• If both of them cheat, then both get low profits (as distinct from very low profits).
  

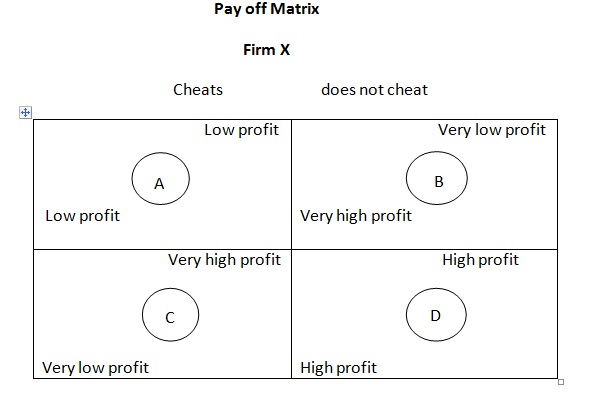
Despite the fact that cheating by both would them mutually worse off, yet decision to cheat would dominate. This is because:
1. If y does not cheat, but it fears that X may cheat, then Y's profits will be very low. However, if Y cheats and X also cheats, Y's profits will be low and hence Y would feel safe in cheating rather than non cheating.
2. If X does not cheat but fears that Y may cheat, then profits of X will be very low. But if X cheats, its profits will only be low. Hence, it would be safe for X to cheat.

As a result both X and Y would cheat. The outcome will be low profits whereas by not cheating both could have earned high profits.
The prisoner's Dilemma thus provides an insight into the oligopolistic behaviour where the outcome of mutual suspicion and uncertainty often results in mutual disadvantage and often results in collapse of cartels